📚 Teaching Graphs

📌 Definition

Graphs are a fundamental data structure in computer science used to model relationships between objects.
Each object is a node (vertex), and the connection between them is an edge (arc).

  • In a complete graph, there is a single edge between every pair of distinct vertices.
  • There are no loops and no multiple edges in such graphs.

📍 Common Uses of Graphs

  • Pathfinding algorithms (e.g., Google Maps, GPS)
  • Web page ranking (e.g., Google’s PageRank algorithm)
  • Network routing (e.g., data packet transfers)

🧠 Warm-Up Activity

Scenario:
You’re an Amazon delivery driver. You have 10 packages to deliver to 10 houses in a neighborhood.

Questions to consider:

  • What strategies would you use to decide where to go first?
  • How do real-life delivery companies solve this problem?
  • Would it be practical to try every possible route? Why or why not?

This activity introduces students to graph-based optimization problems, like the Traveling Salesman Problem (TSP).

🗺️ Graph Representations

✅ Adjacency Matrix

  • A matrix of size n x n (where n is the number of vertices).
  • Stores 0s and 1s:
    • 1 if there’s an edge between two vertices
    • 0 otherwise

Undirected Graph Example:
Each edge is bidirectional: if there’s a connection between vertex i and j, then both matrix[i][j] and matrix[j][i] = 1.

Directed Graph Example:
Connections are one-way: if there’s an edge from i to j, then only matrix[i][j] = 1.

✅ Adjacency List

  • Uses an array of lists to represent which vertices are connected.
  • Each index in the array corresponds to a vertex.
  • Each element in the list is a neighboring vertex.

✅ Completed Hacks

🧠 Warm-Up Activity: Amazon Delivery Driver

Prompt:
Imagine you are a delivery driver for Amazon. You have 10 packages to deliver to 10 different houses in a neighborhood. What’s the best way to plan your route so you don’t waste time and gas?

Response:

To plan the most efficient route, I would:

  • Identify clusters of houses to minimize backtracking.
  • Use a graph to represent houses (nodes) and roads (edges), with edge weights as travel time or distance.
  • Apply a pathfinding algorithm like Dijkstra’s or A* to find the shortest path.
  • Use a heuristic like Nearest Neighbor as a greedy approximation for the Traveling Salesman Problem (TSP).

Why not try every possible route?
There are 10! = 3,628,800 possible permutations, which is computationally inefficient.
Real-world systems use smart heuristics or optimization algorithms to find near-optimal paths quickly.

🍿 Popcorn Hack: Graph Representation of Cities

Prompt:
How can we represent cities and paths as graphs?

Response:

  • Nodes (Vertices): Cities
  • Edges: Roads between the cities
  • Weights on Edges: Could represent distances, tolls, or travel time

Example Graph:

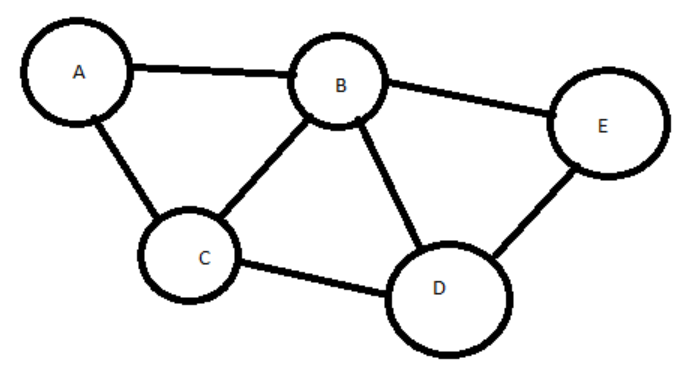
A ↔ B (10 mi) A ↔ C (20 mi) B ↔ D (15 mi) C ↔ D (30 mi) D ↔ E (10 mi)

What can we do with this graph?

  • Evaluate different paths from A to E
  • Use shortest path algorithms to find the optimal route
  • Add or remove roads dynamically to simulate construction or closures

🏠 Homework Hack: College Board Example

Q1:

In which of the configurations is it possible to have redundant routing between devices Q and V?
Answer:
C) Both configuration I and configuration II
Explanation:
Redundant routing exists when multiple paths connect Q and V, which appears in both configurations.

Q2:

In configuration I, what is the minimum number of connections that must be broken or removed before device T can no longer communicate with device U?
Answer:
B) Two
Explanation:
There are at least two distinct paths between T and U. Removing both will isolate communication.

Popcorn hack Heurestics

Setting up the Greedy Coin Change Algorithm 🪙 Greedy Coin Change Algorithm 🔄 Popcorn Hack: Reverse the Greedy Strategy! You’re looking at a greedy algorithm that picks the largest coin first. Try flipping it!

🔁 Change coins = [25, 10, 5, 1] to [1, 5, 10, 25] 🧠 See how it affects the number of coins used 📊 Reflect: is it more or less efficient? Is it perfect? Is it good enough? AP CSP Concepts: Algorithm, Abstraction, Efficiency

def reversed_greedy_coin_change(amount, coins=[1, 5, 10, 25]):
    change = []
    for coin in coins:
        while amount >= coin:
            amount -= coin
            change.append(coin)
    return change

amount = 63
result = reversed_greedy_coin_change(amount)
print(f"Change for {amount}¢ with reversed coins: {result}")
print(f"Total coins used: {len(result)}")

Reflection: More or Less Efficient? → Way less efficient. Instead of 6 coins, you needed 63 coins.

Is it Perfect? → No. Definitely not perfect when you reverse it.

Is it Good Enough? → Nope. It uses many more coins, making it impractical.

⚡Why? Greedy works best when larger coins cover more value quickly.

Homework hacks

Changing the order of coins from largest-to-smallest to smallest-to-largest made the greedy algorithm much worse, using far more coins to make the same amount. The original greedy algorithm (starting with the largest coins) used fewer coins because it quickly covered large parts of the total. Greedy algorithms work well when bigger choices lead naturally to better overall solutions, but they can fail when early choices block better paths later on — showing that order and structure matter when designing algorithms.